Teorema. Probabilitatea sumei evenimentelor incompatibile este egală cu suma probabilităților acestor evenimente:

Corolarul 1. Folosind metoda inducției matematice, formula (3.10) poate fi generalizată la orice număr de evenimente incompatibile pe perechi:

Corolarul 2. Deoarece evenimentele opuse sunt incompatibile, iar suma lor este un eveniment de încredere, atunci, folosind (3.10), avem:

Adesea, atunci când rezolvați probleme, formula (3.12) este utilizată sub forma:

(3.13)

Exemplul 3.29. Într-un experiment cu aruncarea unui zar, găsiți probabilitățile de a obține mai mult de 3 și mai puțin de 6 puncte pe partea superioară.

Să notăm evenimentele asociate cu pierderea unui punct de pe fața superioară a zarului de U 1 , două puncte prin U 2 ,…, la șase puncte U 6 .

Lasă evenimentul U– un număr de puncte mai mare de 3 și mai mic de 6 care apar pe fața de sus a zarului. Acest eveniment va avea loc dacă are loc cel puțin unul dintre evenimente U 4 sau U 5 , prin urmare, poate fi reprezentat ca suma acestor evenimente: . U 4 Pentru că evenimentele U 5 Şi U 1 , U 2 ,…,U 6 sunt inconsecvente, atunci pentru a afla probabilitatea sumei lor folosim formula (3.11). Avand in vedere ca probabilitatile evenimentelor

sunt egali, obtinem: Comentariu.

Cu toate acestea, abordarea clasică a conceptului de probabilitate, spre deosebire de teorema privind probabilitatea unei sume de evenimente incompatibile, este aplicabilă numai pentru rezultate la fel de posibile.

Exemplul 3.30. Probabilitatea ca trăgătorul să lovească ținta este de 0,7. Ce este probabilitatea ca

că trăgătorul nu va lovi ținta?

Fie evenimentul că trăgătorul lovește ținta, apoi evenimentul că trăgătorul nu lovește ținta este evenimentul opus evenimentului, deoarece în urma fiecărui test are loc întotdeauna unul și doar unul dintre aceste evenimente. Folosind formula (3.13), obținem:

3.2.10. Probabilitatea de a avea loc evenimente Definiţie. Evenimentul este numit dependente de la eveniment

3.2.10. Probabilitatea de a avea loc evenimente dacă probabilitatea unui eveniment depinde dacă evenimentul a avut loc sau nu. Se numește probabilitatea unui eveniment calculată având în vedere că evenimentul a avut loc probabilitate condiționată

Teorema. evenimente și este desemnat

Probabilitatea apariției evenimentelor este egală cu produsul dintre probabilitatea unuia dintre ele și probabilitatea condiționată a celuilalt, calculată cu condiția ca primul să fi avut loc: Condiția independenței unui eveniment față de un eveniment poate fi scris sub forma

Din această afirmație rezultă că pentru evenimente independente este valabilă următoarea relație:

sunt egali, obtinem: adică probabilitatea produsului de evenimente independente și este egală cu produsul probabilităților acestora.

Probabilitatea apariției mai multor evenimente este egală cu produsul probabilităților acestor evenimente, iar probabilitatea fiecărui eveniment ulterior în ordine este calculată cu condiția ca toate cele anterioare să fi avut loc:

Dacă evenimentele sunt independente, atunci avem: Exemplul 3.31.

Într-o cutie sunt 5 bile albe și 3 negre. Două bile sunt extrase din el la întâmplare, succesiv, fără înlocuire. Aflați probabilitatea ca ambele bile să fie albe.

Fie ca evenimentul să fie apariția unei mingi albe în timpul primei extrageri și apariția unei mingi albe în timpul celei de-a doua extrageri. Având în vedere că, (probabilitatea apariției unei a doua mingi albe, având în vedere că prima minge extrasă a fost albă și nu a fost returnată în cutie). Deoarece evenimentele sunt dependente, găsim probabilitatea produsului lor folosind formula (3.15): Exemplul 3.32.

Probabilitatea ca primul trăgător să lovească ținta este de 0,8; al doilea – 0,7. Fiecare trăgător a tras într-o țintă. Care este probabilitatea ca cel puțin un trăgător să lovească ținta? Care este probabilitatea ca un trăgător să lovească ținta? Lăsați evenimentul să fie primul trăgător care lovește ținta și al doilea. Toate opțiunile posibile pot fi reprezentate în formular tabelele 3.5, unde „+” înseamnă că

evenimentul s-a petrecut

Fie evenimentul că cel puțin un trăgător lovește ținta Atunci evenimentul este o sumă de evenimente independente și, prin urmare, este imposibil să se aplice teorema asupra probabilității unei sume de evenimente incompatibile în această situație.

Să considerăm evenimentul opus evenimentului care va avea loc atunci când niciun trăgător nu lovește ținta, adică este un produs de evenimente independente. Folosind formulele (3.13) și (3.15), obținem:

Lăsați evenimentul să fie un trăgător care lovește ținta. Acest eveniment poate fi reprezentat astfel:

Evenimente și sunt independente, evenimente și sunt, de asemenea, independente. Evenimente care sunt produse ale evenimentelor și sunt incompatibile. Folosind formulele (3.10) și (3.15) obținem:

Proprietăți ale operațiilor de adunare și înmulțire a evenimentelor:

3.2.11. Formula probabilității totale. Formula Bayes

Fie ca un eveniment să se producă numai împreună cu unul dintre evenimentele incompatibile în perechi (ipoteze),...,, formând un grup complet, i.e.

Probabilitatea unui eveniment se găsește prin formula probabilitate totala:

Dacă evenimentul a avut deja loc, atunci probabilitățile ipotezelor pot fi reestimate folosind formula Bayesian:

(3.17)

Exemplul 3.33. Sunt două urne identice cu bile. Prima urnă conține 5 bile albe și 10 negre, a doua urnă conține 3 bile albe și 7 negre. Ei aleg o urnă la întâmplare și scot o minge din ea.

Găsiți probabilitatea ca această minge să fie albă.

Dintr-o urnă aleasă aleatoriu se extrage o minge albă. Găsiți probabilitatea ca mingea să fie extrasă din prima urnă.

Produsul a două evenimente și numiți un eveniment constând în producerea în comun a acestor evenimente.

Produsul mai multor evenimente numiți un eveniment constând în producerea în comun a tuturor acestor evenimente.

De exemplu, apariția unei steme în trei aruncări simultane de monede.

Probabilitate condiționată

Probabilitate condiționată este probabilitatea ca un eveniment să se producă, calculată în ipoteza că evenimentul a avut deja loc:

Exemplu. În urnă sunt 3 bile albe și 3 negre. Din urnă se scoate câte o minge de două ori fără a le înlocui. Găsiți probabilitatea ca o minge albă să apară în a doua încercare (eveniment), dacă în prima încercare a fost extrasă o minge neagră (eveniment ).

Soluţie. După primul test, în urnă au rămas 5 bile, dintre care 3 sunt albe.

Probabilitatea condiționată necesară

Probabilitate condiționată eveniment, cu condiția ca evenimentul să fi avut deja loc, prin definiție, este egal cu

Teorema înmulțirii probabilităților

Teorema. Probabilitatea apariției comune a două evenimente este egală cu produsul dintre probabilitatea unuia dintre ele și probabilitatea condiționată a celuilalt, calculată în ipoteza că primul eveniment a avut deja loc:

Dovada. Prin definiția probabilității condiționate,

Comentariu. . Un eveniment este echivalent cu un eveniment. Prin urmare,

Şi. (***)

Consecinţă. Probabilitatea producerii comune a mai multor evenimente este egală cu produsul dintre probabilitatea unuia dintre ele și probabilitățile condiționate ale tuturor celorlalte, iar probabilitatea fiecărui eveniment ulterior este calculată în ipoteza că toate evenimentele anterioare au avut deja loc ( în cazul producerii a trei evenimente:

Ordinea în care sunt organizate evenimentele poate fi aleasă în orice mod.

Exemplu. În urnă sunt 5 bile albe, 4 negre și 3 albastre. Se extrage o minge la întâmplare fără a o înlocui, apoi se extrag a doua și a treia minge. Găsiți probabilitatea ca o bilă albă (eveniment) să apară la prima încercare, o bilă neagră (eveniment) la a doua încercare și o bilă albastră (eveniment) la a treia încercare.

Soluţie. Probabilitatea ca o minge albă să apară în prima încercare

Probabilitatea ca o minge neagră să apară în a doua încercare, calculată presupunând că o minge albă a apărut în prima încercare (probabilitate condiționată)

Probabilitatea ca o minge albastră să apară în a treia încercare, calculată în ipoteza că o minge albă a apărut în prima încercare și o minge neagră în a doua (probabilitate condiționată)

Probabilitate necesară

Evenimentul A este numit independent de la evenimentul B dacă probabilitatea evenimentului A nu depinde de faptul dacă evenimentul B are loc sau nu. Evenimentul A este numit Evenimentul este numit de la evenimentul B dacă probabilitatea evenimentului A se modifică în funcție de producerea sau nu a evenimentului B.

Probabilitatea evenimentului A, calculată cu condiția ca evenimentul B să fi avut deja loc, se numește probabilitate condiționată a evenimentului A și se notează .

Condiția pentru independența evenimentului A față de evenimentul B poate fi scrisă ca
.

Teorema înmulțirii probabilităților. Probabilitatea apariției a două evenimente este egală cu produsul dintre probabilitatea unuia dintre ele și probabilitatea condiționată a celuilalt, calculată cu condiția ca primul să fi avut loc:

Dacă evenimentul A nu depinde de evenimentul B, atunci evenimentul B nu depinde de evenimentul A. Mai mult, probabilitatea apariției evenimentelor este egală cu produsul probabilităților acestora:

.

Exemplul 14. Sunt 3 cutii care conțin 10 părți. Prima cutie conține 8, a doua - 7 și a treia - 9 părți standard. O parte este scoasă la întâmplare din fiecare cutie. Aflați probabilitatea ca toate cele trei părți scoase să fie standard.

Probabilitatea ca o parte standard să fie luată din prima casetă (evenimentul A) este egală cu
. Probabilitatea ca o parte standard să fie eliminată din a doua casetă (evenimentul B) este egală cu
. Probabilitatea ca o parte standard să fie eliminată din a treia casetă (evenimentul C) este egală cu
.

Deoarece evenimentele A, B și C sunt colectiv independente, atunci prin teorema înmulțirii probabilitatea necesară este egală cu

Să dăm un exemplu de utilizare în comun a teoremelor de adunare și înmulțire.

Exemplul 15. Probabilitățile de apariție a evenimentelor independente A 1 și A 2 sunt egale cu p 1 și, respectiv, p 2. Găsiți probabilitatea apariției unuia dintre aceste evenimente (evenimentul A). Găsiți probabilitatea de apariție a cel puțin unuia dintre aceste evenimente (evenimentul B).

Să notăm probabilitățile de evenimente opuse Şi prin q 1 =1-p 1 și, respectiv, q 2 =1-p 2.

Evenimentul A va avea loc dacă apare evenimentul A 1 și evenimentul A 2 nu are loc sau dacă apare evenimentul A 2 și evenimentul A 1 nu are loc. Prin urmare,

Evenimentul B va avea loc dacă apare evenimentul A sau dacă evenimentele A 1 și A 2 au loc simultan. Prin urmare,

Probabilitatea evenimentului B poate fi determinată diferit. Eveniment Opusul evenimentului B este că ambele evenimente A 1 și A 2 nu vor avea loc. Prin urmare, folosind teorema înmulțirii probabilităților pentru evenimente independente, obținem

care coincide cu expresia obtinuta mai devreme, deoarece identitatea tine

7. Formula probabilității totale. Formula lui Bayes.

Teorema 1. Să presupunem că evenimentele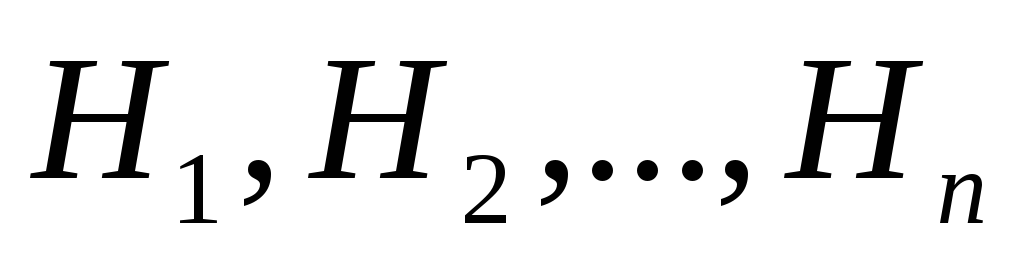
formează un grup complet de evenimente incompatibile în perechi (astfel de evenimente se numesc ipoteze). Fie A un eveniment arbitrar. Apoi probabilitatea evenimentului A poate fi calculată folosind formula

Dovada. Deoarece ipotezele formează un grup complet, atunci , și, prin urmare,.

Datorită faptului că ipotezele sunt evenimente incompatibile în perechi, evenimentele sunt, de asemenea, incompatibile în perechi. Prin teorema adunării probabilităților

Aplicând acum teorema înmulțirii probabilităților, obținem

Formula (1) se numește formula probabilității totale. În formă prescurtată se poate scrie după cum urmează

.

Formula este utilă dacă probabilitățile condiționate ale evenimentului A sunt mai ușor de calculat decât probabilitatea necondiționată.

Exemplul 16. Există 3 pachete de 36 de cărți și 2 pachete de 52 de cărți. Alegem un pachet la întâmplare și o carte din el la întâmplare. Găsiți probabilitatea ca cartea extrasă să fie un as.

Fie A evenimentul că cartea extrasă este un as. Să introducem două ipoteze în considerare:

- o carte este extrasă dintr-un pachet de 36 de cărți,

- se extrage o carte dintr-un pachet de 52 de cărți.

Pentru a calcula probabilitatea evenimentului A, folosim formula probabilității totale:

Teorema 2. Să presupunem că evenimentele
formează un grup complet de evenimente incompatibile pe perechi. Fie A un eveniment arbitrar. Probabilitatea condiționată a ipotezei presupunând că a avut loc evenimentul A, poate fi calculat folosind formula lui Bayes:

Dovada. Din teorema înmulțirii probabilităților pentru evenimente dependente rezultă că .

.

Aplicând formula probabilității totale, obținem (2).

Probabilităţi de ipoteze
se numesc a priori, iar probabilităţile ipotezelor
cu condiția ca evenimentul A să fi avut loc se numesc a posteriori. Formulele lui Bayes în sine sunt numite și formule de probabilitate de ipoteză.

Exemplul 17. Sunt 2 urne. Prima urnă conține 2 bile albe și 4 negre, iar a doua urnă conține 7 bile albe și 5 negre. Alegem o urna la intamplare si tragem o minge din ea la intamplare. S-a dovedit a fi negru (a avut loc evenimentul A). Aflați probabilitatea ca mingea să fi fost extrasă din prima urna (conjectura
). Găsiți probabilitatea ca mingea să fi fost extrasă din a doua urnă (conjectura
).

Să aplicăm formulele lui Bayes:

,

.

Exemplul 18. La fabrică, șuruburile sunt produse de trei mașini, care produc 25%, 35% și, respectiv, 40% din toate șuruburile. Defecte ale produselor acestor mașini sunt de 5%, 4%, respectiv 2%. Un șurub a fost selectat dintre produsele tuturor celor trei mașini. S-a dovedit a fi defect (evenimentul A). Găsiți probabilitatea ca șurubul să fi fost eliberat de prima, a doua, a treia mașină.

Lasă
- evenimentul că șurubul a fost eliberat de prima mașină,
- a doua mașină,
- a treia mașină. Aceste evenimente sunt incompatibile perechi și formează un grup complet. Să folosim formule Bayes

Ca rezultat obținem

,

,

.

Teorema.(Înmulțirea probabilității) Probabilitatea apariției a două evenimente (apariția în comun a acestor evenimente) este egală cu produsul dintre probabilitatea unuia dintre ele și probabilitatea condiționată a celuilalt, calculată cu condiția ca primul eveniment să fi avut deja loc.

De asemenea, puteți scrie:

Demonstrarea acestei teoreme rezultă direct din definiția probabilității condiționate.

Dacă evenimentele sunt independente, atunci , iar teorema înmulțirii probabilităților ia forma:

În cazul producerii mai multor evenimente dependente, probabilitatea este egală cu produsul unuia dintre ele cu probabilitățile condiționate ale tuturor celorlalte, cu condiția ca probabilitatea fiecăruia ulterior să fie calculată în ipoteza că toate celelalte evenimente au deja a avut loc.

Din teorema produsului probabilităților putem concluziona că probabilități aspect cel puțin un eveniment .

Dacă testul poate duce la n evenimente care sunt independente în agregat, atunci probabilitatea apariției a cel puțin unuia dintre ele este egală cu

Eveniment aici O denotă apariția a cel puțin unuia dintre evenimente Ai, O q i– probabilitatea unor evenimente opuse.

Exemplul 1. Dintr-un pachet complet de cărți (52 buc.), patru cărți sunt scoase în același timp. Găsiți probabilitatea ca printre aceste patru cărți să fie cel puțin un diamant sau un cartonaș roșu.

Soluţie.

Să notăm ca eveniment apariția a cel puțin un card diamant O , apariția a cel puțin unui cartonaș roșu este un eveniment ÎN . Astfel, trebuie să determinăm probabilitatea evenimentului CU = O + ÎN .

În plus, evenimente O Pentru că evenimentele ÎN – articulație, adică apariția unuia dintre ele nu exclude apariția celuilalt.

Există un total de 13 inimi și 13 diamante în pachet.

Să găsim probabilitatea unui eveniment opus evenimentului CU (nu vor fi diamante sau inimioare printre cărțile eliminate):

la scoaterea primei cărți, probabilitatea ca nici o carte roșie, nici diamante să nu apară este , la scoaterea a doua carte - , a treia - , a patra - .

Atunci probabilitatea ca printre cărțile extrase să nu fie nici diamante, nici inimi, este egală cu .

Probabilitate necesară

Exemplul 2. Care este probabilitatea ca la aruncarea a trei zaruri să apară 6 puncte pe cel puțin unul dintre zaruri?

Soluţie.

Probabilitatea de a obține 6 puncte la o singură aruncare a zarurilor este de . Probabilitatea de a nu obține 6 puncte este . Probabilitatea ca o aruncare de trei zaruri să nu aibă ca rezultat un 6 este .

Atunci probabilitatea ca 6 puncte să apară cel puțin o dată este egală cu .

Exemplul 3. Cilindrul revolverului conține 4 cartușe din șase în ordine aleatorie. Tamburul este rotit, iar apoi declanșatorul este apăsat de două ori. Aflați probabilitățile de: a) cel puțin o lovitură, b) două lovituri, c) două rateuri.

Soluţie.

Probabilitatea de a declanșa prima dată când trăgaciul este apăsat (eveniment O ) este egal cu , probabilitatea unei rateuri - Probabilitatea unei lovituri atunci când trăgaciul este apăsat pentru a doua oară depinde de rezultatul primei trageri.

Deci, dacă în primul caz a fost o împușcătură, atunci au rămas doar 3 cartușe în tambur și au fost distribuite în 5 sloturi, deoarece când trăgaciul este apăsat pentru a doua oară, fanta în care a fost amplasat cartuşul atunci când trăgaciul a fost apăsat pentru prima dată nu poate fi vizavi de butoi.

Probabilitatea condiționată de o lovitură la a doua încercare - dacă a fost o lovitură prima dată - dacă prima dată a avut loc o rau.

Probabilitatea condiționată a unei rateuri de aprindere a doua oară - dacă s-a produs o împușcare prima dată - dacă a avut loc o rată de aprindere prima dată.

Să luăm în considerare probabilitățile ca în al doilea caz să se producă o împușcătură (eveniment ÎN ) sau va avea loc o rată de foc (eveniment ) cu condiția ca în primul caz să se fi produs o împușcare (eveniment O ) sau rau (eveniment).

Două lovituri la rând

Prima rau, a doua lovitură

Prima lovitură, a doua rau

Două rateuri la rând

Aceste patru cazuri formează un grup complet de evenimente (suma probabilităților lor este egală cu unu)

Analizând rezultatele obținute, vedem că probabilitatea de cel puțin o lovitură este egală cu suma

Exemplul 4. Doi trăgători trag într-o țintă. Probabilitatea de a lovi ținta cu o singură lovitură este de 0,7 pentru primul trăgător și de 0,8 pentru al doilea. Găsiți probabilitatea ca în timpul unei salve doar unul dintre trăgători să lovească ținta.

Soluţie.

Să notăm primul trăgător care lovește ținta ca eveniment A, al doilea ca eveniment B, ratarea primului trăgător ca eveniment și ratarea celui de-al doilea trăgător ca eveniment.

Probabilitatea ca primul trăgător să lovească ținta și al doilea nu este egală cu

Probabilitatea ca al doilea trăgător să lovească ținta și primul nu este egală cu

Atunci probabilitatea de a lovi ținta cu un singur trăgător este

Același rezultat poate fi obținut în alt mod - găsim probabilitățile ca ambii trăgători să lovească ținta și să rateze ambii. Aceste probabilități sunt, respectiv, egale:

Atunci probabilitatea ca un singur trăgător să lovească ținta este:

Exemplul 5. Probabilitatea ca o piesă luată la întâmplare dintr-un anumit lot de piese să fie defectă este de 0,2. Aflați probabilitatea ca din trei părți luate, 2 să nu fie defecte.

Soluţie.

Să notăm o parte defectă ca eveniment A și o parte nedefectă ca eveniment .

Dacă dintre trei părți există doar un defect, atunci acest lucru este posibil într-unul din trei cazuri: piesa defectă va fi prima, a doua sau a treia.

Exemplul 6. Probabilitățile ca partea dorită să fie în prima, a doua, a treia sau a patra casetă sunt 0,6, 0,7, 0,8, respectiv 0,9. Aflați probabilitatea ca această parte să fie situată: a) în cel mult trei casete; b) în cel puţin două casete.

Soluţie.

a) Probabilitatea ca o parte dată să fie în toate cele patru casete este egală cu

Probabilitatea ca piesa dorită să fie în cel mult trei casete este egală cu probabilitatea ca aceasta să nu fie în toate cele patru casete.

b) Probabilitatea ca piesa cerută să fie în cel puțin două casete este suma probabilităților ca piesa să fie în doar două casete, doar trei casete, doar patru casete. Desigur, aceste probabilități pot fi calculate și apoi adunate, cu toate acestea, este mai ușor să faci altfel. Aceeași probabilitate este egală cu probabilitatea ca piesa să nu fie într-o singură cutie și să fie disponibilă deloc.

Atunci când evaluăm probabilitatea apariției oricărui eveniment aleatoriu, este foarte important să înțelegem bine dacă probabilitatea (probabilitatea unui eveniment) de apariție a evenimentului care ne interesează depinde de modul în care se dezvoltă alte evenimente. În cazul schemei clasice, când toate rezultatele sunt la fel de probabile, putem deja estima independent valorile probabilității evenimentului individual care ne interesează. Putem face acest lucru chiar dacă evenimentul este o colecție complexă de mai multe rezultate elementare. Ce se întâmplă dacă mai multe evenimente întâmplătoare apar simultan sau secvenţial? Cum afectează acest lucru probabilitatea ca evenimentul care ne interesează să se întâmple? Dacă arunc un zar de mai multe ori și vreau să apară un șase și tot am ghinion, înseamnă asta că ar trebui să-mi măresc pariul pentru că, conform teoriei probabilităților, sunt pe cale să am noroc? Din păcate, teoria probabilității nu afirmă așa ceva. Nici zarurile, nici cărțile, nici monedele nu își pot aminti ce ne-au arătat ultima dată. Pentru ei nu contează deloc dacă este prima sau a zecea oară când îmi testez norocul astăzi. De fiecare dată când repet rulada, știu un singur lucru: și de data aceasta probabilitatea de a obține un șase este din nou de o șesime. Desigur, asta nu înseamnă că numărul de care am nevoie nu va apărea niciodată. Asta înseamnă doar că pierderea mea după prima aruncare și după orice altă aruncare sunt evenimente independente. Evenimentele A și B sunt numite independente dacă apariția unuia dintre ele nu afectează în niciun fel probabilitatea celuilalt eveniment. De exemplu, probabilitățile de a lovi o țintă cu prima dintre cele două arme nu depind de dacă ținta a fost lovită de cealaltă armă, astfel încât evenimentele „prima armă a lovit ținta” și „a doua armă a lovit ținta” sunt independent. Dacă două evenimente A și B sunt independente și probabilitatea fiecăruia dintre ele este cunoscută, atunci probabilitatea apariției simultane atât a evenimentului A, cât și a evenimentului B (notat AB) poate fi calculată folosind următoarea teoremă.

Teorema înmulțirii probabilităților pentru evenimente independente

P(AB) = P(A)*P(B) probabilitatea apariției simultane a două evenimente independente este egală cu produsul probabilităților acestor evenimente.

Exemplul 1. Probabilitățile de lovire a țintei la tragerea cu primul și respectiv al doilea tun sunt egale: p 1 = 0,7; p2 = 0,8. Găsiți probabilitatea unei lovituri cu o salvă de ambele arme simultan.

după cum am văzut deja, evenimentele A (loviți de prima armă) și B (loviți de a doua armă) sunt independente, adică. P(AB)=P(A)*P(B)=p1*p2=0,56.

Exemplul 2. Ce se întâmplă cu estimările noastre dacă evenimentele inițiale nu sunt independente? Să schimbăm puțin exemplul anterior.

Doi trăgători trag în ținte la o competiție, iar dacă unul dintre ei trage cu precizie, adversarul începe să devină nervos și rezultatele sale se înrăutățesc. Cum să transformi această situație de zi cu zi într-o problemă matematică și să schițezi modalități de a o rezolva? Este intuitiv clar că este necesar să se separe cumva cele două opțiuni pentru desfășurarea evenimentelor, pentru a crea în esență două scenarii, două sarcini diferite. În primul caz, dacă adversarul a ratat, scenariul va fi favorabil sportivului nervos și precizia acestuia va fi mai mare. În al doilea caz, dacă adversarul și-a luat șansa decent, probabilitatea de a lovi ținta pentru al doilea sportiv scade.

Exemplul 3. Pentru a separa posibilele scenarii (numite adesea ipoteze) pentru desfășurarea evenimentelor, vom folosi adesea o diagramă „arborele probabilității”. Această diagramă este similară ca semnificație cu arborele de decizie cu care probabil v-ați ocupat deja. Fiecare ramură reprezintă un scenariu separat pentru desfășurarea evenimentelor, doar că acum are propria sa valoare a așa-numitei probabilități condiționate (q 1, q 2, q 1 -1, q 2 -1).

Această schemă este foarte convenabilă pentru analiza evenimentelor aleatoare secvențiale. Încă o întrebare importantă rămâne de clarificat: de unde provin probabilitățile inițiale în situații reale? La urma urmei, teoria probabilității nu funcționează doar cu monede și zaruri? De obicei, aceste estimări sunt luate din statistici, iar când informațiile statistice nu sunt disponibile, ne desfășurăm propriile cercetări. Și adesea trebuie să începem nu cu colectarea datelor, ci cu întrebarea de ce informații avem de fapt nevoie.

Sa presupunem ca trebuie sa estimam intr-un oras cu o populatie de o suta de mii de locuitori volumul pietei pentru un produs nou care nu este un articol esential, de exemplu, pentru un balsam pentru ingrijirea parului vopsit. Să luăm în considerare diagrama „arborele probabilității”. În acest caz, trebuie să estimăm aproximativ valoarea probabilității pe fiecare „ramură”. Deci, estimările noastre privind capacitatea pieței:

1) din toți locuitorii orașului, 50% sunt femei,

2) dintre toate femeile, doar 30% își vopsesc părul des,

3) dintre ei, doar 10% folosesc balsamuri pentru părul vopsit,

Conform legii înmulțirii probabilităților, determinăm probabilitatea evenimentului care ne interesează A = (un locuitor al orașului cumpără acest nou balsam de la noi) = 0,00045. Să înmulțim această valoare a probabilității cu numărul de locuitori ai orașului. Drept urmare, avem doar 45 de clienți potențiali, iar având în vedere că o sticlă din acest produs durează câteva luni, comerțul nu este foarte animat. Și totuși există un anumit beneficiu din evaluările noastre. În primul rând, putem compara previziunile diferitelor idei de afaceri, acestea vor avea diferite „furci” în diagrame și, desigur, valorile probabilității vor fi, de asemenea, diferite. În al doilea rând, așa cum am spus deja, o variabilă aleatoare nu se numește aleatoare deoarece nu depinde deloc de nimic. Doar ea valoarea exacta necunoscut dinainte. Știm că numărul mediu de cumpărători poate fi crescut (de exemplu, prin promovarea unui produs nou). Așadar, este logic să ne concentrăm eforturile asupra acelor „furci” în care distribuția probabilității nu ni se potrivește în mod special, asupra acelor factori pe care suntem capabili să-i influențăm. Să ne uităm la un alt exemplu cantitativ de cercetare a comportamentului consumatorilor.

Exemplul 3.În medie, 10.000 de oameni vizitează piața alimentară pe zi. Probabilitatea ca un vizitator al pieței să intre în pavilionul de produse lactate este de 1/2. Se știe că acest pavilion vinde în medie 500 kg de diverse produse pe zi. Putem spune că achiziția medie în pavilion cântărește doar 100 g?

Discuţie.

Desigur că nu. Este clar că nu toți cei care au intrat în pavilion au ajuns să cumpere ceva de acolo.

După cum se arată în diagramă, pentru a răspunde la întrebarea despre greutatea medie a unei achiziții, trebuie să găsim un răspuns la întrebarea care este probabilitatea ca o persoană care intră în pavilion să cumpere ceva acolo. Dacă nu avem astfel de date la dispoziție, dar avem nevoie de ele, va trebui să le obținem noi înșine observând vizitatorii pavilionului o perioadă de timp. Să presupunem că observațiile noastre au arătat că doar o cincime dintre vizitatorii pavilionului cumpără ceva.

Odată ce am obținut aceste estimări, sarcina devine simplă. Din 10.000 de persoane care vin în piață, 5.000 vor merge la pavilionul de produse lactate vor fi doar 1.000 de achiziții. Greutatea medie a unei achiziții este de 500 de grame. Este interesant de observat că, pentru a construi o imagine completă a ceea ce se întâmplă, logica „ramificării” condiționate trebuie definită în fiecare etapă a raționamentului nostru la fel de clar ca și cum am lucra cu o situație „specifică”, și nu cu probabilităţi.

1. Să existe un circuit electric format din n elemente conectate în serie, fiecare dintre ele funcționând independent de celelalte. Probabilitatea p de defectare a fiecărui element este cunoscută. Determinați probabilitatea de funcționare corectă a întregii secțiuni a circuitului (eveniment A).

2. Elevul știe 20 din 25 întrebări de examen. Găsiți probabilitatea ca elevul să cunoască cele trei întrebări care i-au fost adresate de examinator.

3. Producția constă din patru etape succesive, la fiecare din care funcționează echipamente, pentru care probabilitățile de defecțiune în luna următoare sunt egale cu p 1, p 2, p 3 și, respectiv, p 4. Găsiți probabilitatea ca într-o lună să nu existe întreruperi de producție din cauza defecțiunii echipamentelor.