Cum să găsiți aria unei figuri delimitate de grafice de funcții. Cum se calculează aria unei figuri plane folosind o integrală dublă? În acest caz

În acest articol veți învăța cum să găsiți aria unei figuri, limitat de linii, folosind calcule folosind integrale. Formularea unei astfel de probleme o întâlnim mai întâi în liceu, când tocmai am finalizat studiul integralelor definite și este timpul să începem interpretarea geometrică a cunoștințelor dobândite în practică.

Deci pentru ce este necesar solutie de succes probleme pentru a găsi aria unei figuri folosind integrale:

• Abilitatea de a realiza desene competente;
• Abilitatea de a rezolva o integrală definită folosind binecunoscuta formulă Newton-Leibniz;
• Abilitatea de a „vedea” o opțiune de soluție mai profitabilă - de ex. înțelegeți cum va fi mai convenabil să efectuați integrarea într-un caz sau altul? De-a lungul axei x (OX) sau a axei y (OY)?
• Ei bine, unde am fi fără calcule corecte?) Aceasta include înțelegerea cum să rezolvăm acel alt tip de integrale și calcule numerice corecte.

Algoritm pentru rezolvarea problemei de calcul a ariei unei figuri delimitate de linii:

1. Construim un desen. Este indicat să faceți acest lucru pe o foaie de hârtie în carouri, la scară mare. Semnăm numele acestei funcții cu un creion deasupra fiecărui grafic. Semnarea graficelor se face numai pentru confortul calculelor ulterioare. După ce a primit un grafic al cifrei dorite, în majoritatea cazurilor va fi imediat clar ce limite de integrare vor fi utilizate. Astfel, rezolvăm problema grafic. Cu toate acestea, se întâmplă ca valorile limitelor să fie fracționale sau iraționale. Prin urmare, puteți face calcule suplimentare, treceți la pasul doi.

2. Dacă limitele de integrare nu sunt specificate în mod explicit, atunci găsim punctele de intersecție ale graficelor între ele și vedem dacă soluția noastră grafică coincide cu cea analitică.

3. Apoi, trebuie să analizați desenul. În funcție de modul în care sunt aranjate graficele funcțiilor, există diferite abordări pentru a găsi aria unei figuri. Să luăm în considerare exemple diferite la găsirea ariei unei figuri folosind integrale.

3.1. Cea mai clasică și simplă versiune a problemei este atunci când trebuie să găsiți zona unui trapez curbat. Ce este un trapez curbat? Aceasta este o figură plată limitată de axa x (y = 0), Drept x = a, x = b iar orice curbă continuă pe intervalul de la o la b. În plus, această cifră nu este negativă și nu se află sub axa x. În acest caz, aria trapezului curbiliniu este egală numeric cu integrală definită, calculat folosind formula Newton-Leibniz:

Exemplul 1 y = x2 – 3x + 3, x = 1, x = 3, y = 0.

Prin ce linii este delimitată figura? Avem o parabolă y = x2 – 3x + 3, care este situat deasupra axei OH, este nenegativ, deoarece toate punctele acestei parabole au valori pozitive. Apoi, date linii drepte x = 1Şi x = 3, care sunt paralele cu axa Op-amp, sunt liniile de delimitare ale figurii din stânga și dreapta. Bine y = 0, este și axa x, care limitează figura de jos. Figura rezultată este umbrită, așa cum se poate vedea din figura din stânga. În acest caz, puteți începe imediat să rezolvați problema. În fața noastră este un exemplu simplu de trapez curbat, pe care îl rezolvăm în continuare folosind formula Newton-Leibniz.

3.2. În paragraful anterior 3.1, am examinat cazul în care un trapez curbat este situat deasupra axei x. Acum luați în considerare cazul în care condițiile problemei sunt aceleași, cu excepția faptului că funcția se află sub axa x. La formula standard Newton-Leibniz se adaugă un minus. Vom analiza mai jos cum să rezolvăm o astfel de problemă.

Exemplul 2 . Calculați aria unei figuri delimitate de linii y = x2 + 6x + 2, x = -4, x = -1, y = 0.

ÎN în acest exemplu avem o parabolă y = x2 + 6x + 2, care provine din axă OH, Drept x = -4, x = -1, y = 0. Aici y = 0 limitează cifra dorită de sus. Direct x = -4Şi x = -1 acestea sunt limitele în care se va calcula integrala definită. Principiul rezolvării problemei găsirii ariei unei figuri coincide aproape complet cu exemplul numărul 1. Singura diferență este că funcţie dată nu pozitiv, și încă continuu pe interval [-4; -1] . Ce vrei sa spui ca nu pozitiv? După cum se poate observa din figură, figura care se află în x-urile date are coordonate exclusiv „negative”, ceea ce trebuie să vedem și să ne amintim atunci când rezolvăm problema. Căutăm aria figurii folosind formula Newton-Leibniz, doar cu semnul minus la început.

Articolul nu este completat.

În această lecție vom învăța să calculăm zonele figurilor plane care sunt numite trapezoizi curbilinii .

Exemple de astfel de cifre sunt în figura de mai jos.

Pe de o parte, găsirea ariei unei figuri plane folosind o integrală definită este extrem de simplă. Vorbim despre aria unei figuri, care este limitată de sus de o anumită curbă, de jos de axa absciselor ( Bou), iar în stânga și în dreapta sunt niște linii drepte. Simplitatea este că integrala definită a funcției căreia îi este dată curba este aria unei astfel de figuri(trapez curbiliniu).

Pentru a calcula aria unei figuri avem nevoie de:

1. Integrală definită a funcției care definește curba , care limitează de sus trapezul curbat. Și aici apare prima nuanță semnificativă: un trapez curbat poate fi limitat de o curbă nu numai de sus, ci și de jos . Cum se procedează în acest caz? Simplu, dar important de reținut: integrala în acest caz este luată cu semnul minus .
2. Limitele integrării oŞi b, pe care îl găsim din ecuațiile dreptelor care delimitează figura din stânga și dreapta: x = o , x = b, Unde oŞi b- numere.

Separat, despre mai multe nuanțe.

Curba care delimitează trapezul curbat în partea de sus (sau de jos) trebuie să fie graficul unei funcții continue și nenegative y = f(x) .

Valorile „x” trebuie să aparțină segmentului [o, b] . Adică, nu sunt luate în considerare linii precum tăietura unei ciuperci, a căror tulpină se potrivește bine în acest segment, iar capacul este mult mai lat.

Segmentele laterale pot degenera în puncte . Dacă vedeți o astfel de figură în desen, acest lucru nu ar trebui să vă încurce, deoarece acest punct își are întotdeauna valoarea pe axa „x”. Aceasta înseamnă că totul este în ordine cu limitele integrării.

Acum puteți trece la formule și calcule. Deci zona s trapezul curbat poate fi calculat folosind formula

Dacă f(x) ≤ 0 (graficul funcției este situat sub axă Bou), Asta zona unui trapez curbat poate fi calculat folosind formula

Există, de asemenea, cazuri când atât granițele superioare, cât și cele inferioare ale figurii sunt funcții y = f(x) Şi y = φ (x) , atunci aria unei astfel de cifre este calculată prin formula

. (3)

Rezolvarea problemelor împreună

Să începem cu cazurile în care aria unei figuri poate fi calculată folosind formula (1).

Exemplul 1.Bou) și drept x = 1 , x = 3 .

Soluţie. Deoarece y = 1/x> 0 pe segment, atunci aria trapezului curbiliniu este găsită folosind formula (1):

.

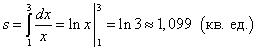Exemplul 2. Găsiți aria figurii delimitată de graficul funcției, linie x= 1 și axa x ( Bou ).

Soluţie. Rezultatul aplicării formulei (1):

Dacă atunci s= 1/2; dacă atunci s= 1/3 etc.

Exemplul 3. Găsiți aria figurii delimitată de graficul funcției, axa absciselor ( Bou) și drept x = 4 .

Soluţie. Figura corespunzătoare condițiilor problemei este un trapez curbiliniu în care segmentul din stânga a degenerat într-un punct. Limitele de integrare sunt 0 și 4. Deoarece, folosind formula (1) găsim aria trapezului curbiliniu:

.

Exemplul 4. Găsiți aria figurii delimitată de liniile , , și situată în primul trimestru.

Soluţie. Pentru a folosi formula (1), să ne imaginăm aria figurii dată de condițiile exemplului ca suma ariilor triunghiului OABși trapez curbat ABC. Când se calculează aria unui triunghi OAB limitele integrării sunt abscisele punctelor OŞi O, iar pentru figură ABC- abscisele punctelor OŞi C (O este punctul de intersecție al dreptei O.A.și parabole și C- punctul de intersecție al parabolei cu axa Bou). Rezolvând împreună (ca sistem) ecuațiile unei drepte și ale unei parabole, obținem (abscisa punctului O) și (abscisa altui punct de intersecție a dreptei și a parabolei, care nu este necesară pentru soluție). În mod similar, obținem , (abscise de puncte CŞi D). Acum avem tot ce ne trebuie pentru a găsi aria unei figuri. Găsim:

Exemplul 5. Găsiți aria unui trapez curbat ACDB, dacă ecuația curbei CDși abscisele OŞi B 1 și respectiv 2.

Soluţie. Să exprimăm această ecuație a curbei prin joc: aria trapezului curbiliniu se găsește folosind formula (1):

.

Să trecem la cazurile în care aria unei figuri poate fi calculată folosind formula (2).

Exemplul 6. Găsiți aria figurii delimitată de parabolă și axa x ( Bou ).

Soluţie. Această cifră este situată sub axa x. Prin urmare, pentru a calcula aria sa, vom folosi formula (2). Limitele de integrare sunt abscisa și punctele de intersecție ale parabolei cu axa Bou. Prin urmare,

Exemplul 7. Găsiți aria cuprinsă între axa absciselor ( Bou) și două unde sinusoidale adiacente.

Soluţie. Zona acestei figuri poate fi găsită folosind formula (2):

.

Să găsim fiecare termen separat:

.

.

În sfârșit găsim zona:

.

Exemplul 8. Găsiți aria figurii cuprinsă între parabolă și curbă.

Soluţie. Să exprimăm ecuațiile de linii prin joc:

Aria conform formulei (2) se obtine ca

,

Unde oŞi b- abscisele punctelor OŞi B. Să le găsim rezolvând împreună ecuațiile:

În sfârșit găsim zona:

Și, în sfârșit, cazurile în care aria unei figuri poate fi calculată folosind formula (3).

Exemplul 9. Găsiți aria figurii cuprinsă între parabole Și .

Introduceți funcția pentru care trebuie să găsiți integrala

Calculatorul oferă soluții DETALIATE pentru integrale definite.

Acest calculator găsește o soluție la integrala definită a funcției f(x) cu limite superioare și inferioare date.

Exemple

Folosind gradul
(pătrat și cub) și fracții

(x^2 - 1)/(x^3 + 1)

Rădăcină pătrată

Sqrt(x)/(x + 1)

Rădăcină cubă

Cbrt(x)/(3*x + 2)

Folosind sinus și cosinus

2*sin(x)*cos(x)

arcsinus

X*arcsin(x)

arc cosinus

X*arccos(x)

Aplicarea logaritmului

X*log(x, 10)

Logaritmul natural

Expozant

Tg(x)*sin(x)

Cotangentă

Ctg(x)*cos(x)

Fracții iraționale

(sqrt(x) - 1)/sqrt(x^2 - x - 1)

Arctangent

X*arctg(x)

Arccotangent

X*arсctg(x)

Sinus și cosinus hiperbolic

2*sh(x)*ch(x)

Tangenta hiperbolica si cotangente

Ctgh(x)/tgh(x)

Arcsinus și arccosinus hiperbolic

X^2*arcsinh(x)*arccosh(x)

Arctangentă și arctangentă hiperbolice

X^2*arctgh(x)*arctgh(x)

Reguli de introducere a expresiilor și funcțiilor

Expresiile pot consta din funcții (notațiile sunt date în ordine alfabetică): absolut (x) Valoare absolută x
(modul x sau |x|) arccos(x) Funcția - arc cosinus al x arccosh(x) Arc cosinus hiperbolic de la x arcsin(x) Arcsine din x arcsinh(x) Arcsin hiperbolic din x arctan(x) Funcția - arctangent de x arctgh(x) Arctangent hiperbolic din x e e un număr care este aproximativ egal cu 2,7 exp(x) Funcție - exponent al x(ca e^x) log(x) sau ln(x) Logaritmul natural al x
(A obține log7(x), trebuie să introduceți log(x)/log(7) (sau, de exemplu, pentru log10(x)=log(x)/log(10)) pi Numărul este „Pi”, care este aproximativ egal cu 3,14 sin(x) Funcția - Sinus de x cos(x) Funcția - Cosinus de x sinh(x) Funcție - Sinus hiperbolic de la x cosh(x) Funcție - Cosinus hiperbolic de la x sqrt(x) Funcția - rădăcină pătrată a x sqr(x) sau x^2 Funcție - Pătrat x tan(x) Functie - Tangenta de la x tgh(x) Functie - Tangenta hiperbolica de la x cbrt(x) Funcție - rădăcină cubă a x

Următoarele operații pot fi utilizate în expresii: Numerele reale intra ca 7.5 , Nu 7,5 2*x- înmulțirea 3/x- diviziune x^3- exponentiarea x+7- adaos x - 6- scăderea
Alte caracteristici: podea(x) Funcție - rotunjire xîn jos (exemplu etaj(4,5)==4,0) plafon (x) Funcție - rotunjire xîn sus (exemplu plafon (4,5)==5,0) semn(x) Funcție - Semn x erf(x) Funcție de eroare (sau integrală de probabilitate) laplace(x) Funcția Laplace

De fapt, pentru a găsi aria unei figuri, nu aveți nevoie de atâtea cunoștințe despre integrala nedefinită și definită. Sarcina „calculați suprafața folosind o integrală definită” implică întotdeauna construirea unui desen, cu atât mai mult problemă de actualitate vor fi cunoștințele și abilitățile tale în desen. În acest sens, este util să vă reîmprospătați memoria graficelor principale functii elementare, și, cel puțin, să fie capabil să construiască o linie dreaptă și o hiperbolă.

Un trapez curbat este o figură plată delimitată de o axă, linii drepte și graficul unei funcții continuă pe un segment care nu își schimbă semnul în acest interval. Fie localizată această cifră nu mai jos axa x:

Apoi aria unui trapez curbiliniu este numeric egală cu o integrală definită. Orice integrală definită (care există) are o semnificație geometrică foarte bună.

Din punct de vedere al geometriei, integrala definită este AREA.

adica o anumită integrală (dacă există) corespunde geometric cu aria unei anumite figuri. De exemplu, luați în considerare integrala definită. Integrandul definește o curbă pe planul situat deasupra axei (cei care doresc pot face un desen), iar integrala definită însăși este numeric egal cu suprafata trapezul curbat corespunzător.

Exemplul 1

Aceasta este o declarație tipică de atribuire. Primul și cel mai important punct al deciziei este construcția desenului. Mai mult, desenul trebuie construit CORECT.

Când construiți un desen, vă recomand următoarea ordine: la început este mai bine să construiți toate liniile drepte (dacă există) și numai Apoi- parabole, hiperbole, grafice ale altor funcții. Este mai profitabil să construiești grafice ale funcțiilor punct cu punct.

În această problemă, soluția ar putea arăta astfel.
Să desenăm desenul (rețineți că ecuația definește axa):

Pe segment se află graficul funcției deasupra axei, De aceea:

Răspuns:

După ce sarcina este finalizată, este întotdeauna util să priviți desenul și să vă dați seama dacă răspunsul este real. În acest caz, „prin ochi” numărăm numărul de celule din desen - ei bine, vor fi aproximativ 9, se pare că este adevărat. Este absolut clar că dacă am primit, să zicem, răspunsul: 20 de unități pătrate, atunci este evident că s-a făcut o greșeală undeva - 20 de celule evident nu se încadrează în figura în cauză, cel mult o duzină. Dacă răspunsul este negativ, atunci și sarcina a fost rezolvată incorect.

Exemplul 3

Calculați aria figurii delimitată de linii și axe de coordonate.

Soluţie: Hai să facem un desen:

Dacă este localizat un trapez curbat sub ax(sau cel putin nu mai sus axa dată), atunci aria sa poate fi găsită folosind formula:

În acest caz:

Atenţie! Cele două tipuri de sarcini nu trebuie confundate:

1) Dacă vi se cere să rezolvați pur și simplu o integrală definită fără niciuna sens geometric, atunci poate fi negativ.

2) Dacă vi se cere să găsiți aria unei figuri folosind o integrală definită, atunci aria este întotdeauna pozitivă! De aceea apare minusul în formula tocmai discutată.

În practică, cel mai adesea figura este situată atât în ​​semiplanul superior, cât și în cel inferior și, prin urmare, de la cele mai simple probleme școlare trecem la exemple mai semnificative.

Exemplul 4

Aflați aria unei figuri plane delimitată de liniile , .

Soluţie: Mai întâi trebuie să finalizați desenul. În general, atunci când construim un desen în probleme de zonă, suntem cel mai interesați de punctele de intersecție a liniilor. Să găsim punctele de intersecție ale parabolei și ale dreptei. Acest lucru se poate face în două moduri. Prima metodă este analitică. Rezolvam ecuatia:

Aceasta înseamnă că limita inferioară a integrării este , limita superioară a integrării este .

Dacă este posibil, este mai bine să nu utilizați această metodă..

Este mult mai profitabil și mai rapid să construiești linii punct cu punct, iar limitele integrării devin clare „de la sine”. Cu toate acestea, metoda analitică de găsire a limitelor mai trebuie folosită uneori dacă, de exemplu, graficul este suficient de mare sau construcția detaliată nu a evidențiat limitele integrării (pot fi fracționale sau iraționale). Și vom lua în considerare și un astfel de exemplu.

Să revenim la sarcina noastră: este mai rațional să construim mai întâi o linie dreaptă și abia apoi o parabolă. Să facem desenul:

Și acum formula de lucru : Dacă există o funcție continuă pe segment mai mare sau egal cu unele funcție continuă, atunci aria figurii limitată de graficele acestor funcții și liniile , , poate fi găsită folosind formula:

Aici nu mai trebuie să vă gândiți la locul în care se află figura - deasupra axei sau sub axa și, aproximativ vorbind, contează care grafic este MAI MARE(față de alt grafic), și care este JOS.

În exemplul luat în considerare, este evident că pe segment parabola este situată deasupra liniei drepte și, prin urmare, este necesar să se scadă din

Soluția finalizată ar putea arăta astfel:

Cifra dorită este limitată de o parabolă deasupra și de o linie dreaptă dedesubt.
Pe segment, conform formulei corespunzătoare:

Răspuns:

Exemplul 4

Calculați aria figurii delimitată de liniile , , , .

Soluţie: Mai întâi, să facem un desen:

Figura a cărei zonă trebuie să o găsim este umbrită în albastru(uitați-vă cu atenție la starea - cum este limitată cifra!). Dar, în practică, din cauza neatenției, apare adesea un „glitch” în care trebuie să găsiți zona unei figuri care este umbrită. verde!

Acest exemplu este util și prin faptul că calculează aria unei figuri folosind două integrale definite.

într-adevăr:

1) Pe segmentul de deasupra axei se află un grafic al unei drepte;

2) Pe segmentul de deasupra axei există un grafic al unei hiperbole.

Este destul de evident că zonele pot (și ar trebui) să fie adăugate, prin urmare:

Cum se calculează volumul unui corp de rotațiefolosind o integrală definită?

Imaginează-ți o figură plată pe planul de coordonate. Noi i-am găsit deja zona. Dar, în plus, această cifră poate fi, de asemenea, rotită și rotită în două moduri:

În jurul axei x;

În jurul axei y .

Acest articol va examina ambele cazuri. A doua metodă de rotație este deosebit de interesantă, ea provoacă cele mai multe dificultăți, dar de fapt soluția este aproape aceeași ca în rotația mai comună în jurul axei x.

Să începem cu cel mai popular tip de rotație.

Să trecem la considerarea aplicațiilor calculului integral. În această lecție vom analiza sarcina tipică și cea mai comună calcularea ariei unei figuri plane folosind o integrală definită. În cele din urmă, să-l găsească pe toți cei care caută sens în matematica superioară. Nu se știe niciodată. Va trebui să o aducem mai aproape în viață teren cabana de vara funcții elementare și găsiți-i aria folosind o integrală definită.

Pentru a stăpâni cu succes materialul, trebuie să:

1) Înțelegeți integrala nedefinită cel puțin la un nivel intermediar. Astfel, manechinii ar trebui să citească mai întâi lecția Nu.

2) Să fie capabil să aplice formula Newton-Leibniz și să calculeze integrala definită. Puteți stabili relații prietenoase calde cu anumite integrale de pe pagină Integrală definită. Exemple de soluții. Sarcina „calculați suprafața folosind o integrală definită” implică întotdeauna construirea unui desen, așa că cunoștințele și abilitățile tale de desen vor fi, de asemenea, o problemă relevantă. Cel puțin, trebuie să fiți capabil să construiți o linie dreaptă, o parabolă și o hiperbolă.

Să începem cu un trapez curbat. Un trapez curbat este o figură plată delimitată de graficul unei anumite funcții y = f(x), axa BOUși linii x = o; x = b.

Aria unui trapez curbiliniu este numeric egală cu o integrală definită

Orice integrală definită (care există) are o semnificație geometrică foarte bună. În clasă Integrală definită. Exemple de soluții am spus că o integrală determinată este un număr. Și acum este timpul să mai spunem una fapt util. Din punct de vedere al geometriei, integrala definită este AREA. adica integrala definită (dacă există) corespunde geometric cu aria unei anumite figuri. Luați în considerare integrala definită

Integrand

definește o curbă pe plan (poate fi desenată dacă se dorește), iar integrala definită în sine este egală numeric cu aria trapezului curbiliniu corespunzător.

Exemplul 1

, , , .

Aceasta este o declarație tipică de atribuire. Cel mai important punct al deciziei este construcția desenului. Mai mult, desenul trebuie construit CORECT.

Când construiți un desen, vă recomand următoarea ordine: la început este mai bine să construiți toate liniile drepte (dacă există) și numai Apoi– parabole, hiperbole, grafice ale altor funcții. Tehnica de construcție punct cu punct poate fi găsită în materialul de referință Grafice și proprietăți ale funcțiilor elementare. Acolo puteți găsi și material foarte util pentru lecția noastră - cum să construiți rapid o parabolă.

În această problemă, soluția ar putea arăta astfel.

Să facem desenul (rețineți că ecuația y= 0 specifică axa BOU):

Nu vom umbri un trapez curbat aici este evident ce zonă despre care vorbim. Solutia continua asa:

Pe segmentul [-2; 1] graficul funcției y = x 2 + 2 localizate deasupra axeiBOU, De aceea:

Răspuns: .

Care are dificultăți în calcularea integralei definite și aplicarea formulei Newton-Leibniz

,

referiți la prelegere Integrală definită. Exemple de soluții. După ce sarcina este finalizată, este întotdeauna util să priviți desenul și să vă dați seama dacă răspunsul este real. În acest caz, numărăm numărul de celule din desen „cu ochi” - ei bine, vor fi aproximativ 9, se pare că este adevărat. Este absolut clar că dacă am primit, să zicem, răspunsul: 20 de unități pătrate, atunci este evident că s-a făcut o greșeală undeva - 20 de celule evident nu se încadrează în figura în cauză, cel mult o duzină. Dacă răspunsul este negativ, atunci și sarcina a fost rezolvată incorect.

Exemplul 2

Calculați aria unei figuri delimitate de linii xy = 4, x = 2, x= 4 și axa BOU.

Acesta este un exemplu de rezolvat singur. Soluție completă și răspuns la sfârșitul lecției.

Ce trebuie să faceți dacă este localizat trapezul curbat sub axBOU?

Exemplul 3

Calculați aria unei figuri delimitate de linii y = e-x, x= 1 și axele de coordonate.

Soluție: Să facem un desen:

Dacă un trapez curbat complet situat sub ax BOU , atunci aria sa poate fi găsită folosind formula:

În acest caz:

.

Atenţie! Cele două tipuri de sarcini nu trebuie confundate:

1) Dacă vi se cere să rezolvați pur și simplu o integrală definită fără nicio semnificație geometrică, atunci aceasta poate fi negativă.

2) Dacă vi se cere să găsiți aria unei figuri folosind o integrală definită, atunci aria este întotdeauna pozitivă! De aceea apare minusul în formula tocmai discutată.

În practică, cel mai adesea figura este situată atât în ​​semiplanul superior, cât și în cel inferior și, prin urmare, de la cele mai simple probleme școlare trecem la exemple mai semnificative.

Exemplul 4

Găsiți aria unei figuri plane delimitată de drepte y = 2x – x 2 , y = -x.

Soluție: Mai întâi trebuie să faci un desen. Când construim un desen în probleme de zonă, suntem cel mai interesați de punctele de intersecție a liniilor. Să găsim punctele de intersecție ale parabolei y = 2x – x 2 și drept y = -x. Acest lucru se poate face în două moduri. Prima metodă este analitică. Rezolvam ecuatia:

Aceasta înseamnă că limita inferioară a integrării o= 0, limita superioară a integrării b= 3. Este adesea mai profitabil și mai rapid să construiești linii punct cu punct, iar limitele integrării devin clare „de la sine”. Cu toate acestea, metoda analitică de găsire a limitelor mai trebuie folosită uneori dacă, de exemplu, graficul este suficient de mare sau construcția detaliată nu a evidențiat limitele integrării (pot fi fracționale sau iraționale). Să revenim la sarcina noastră: este mai rațional să construim mai întâi o linie dreaptă și abia apoi o parabolă. Să facem desenul:

Să repetăm ​​că atunci când construim punctual, limitele integrării sunt cel mai adesea determinate „automat”.

Și acum formula de lucru:

Dacă pe segmentul [ o; b] oarecare funcție continuă f(x) mai mare sau egal cu vreo funcție continuă g(x), atunci aria figurii corespunzătoare poate fi găsită folosind formula:

Aici nu mai trebuie să vă gândiți unde se află figura - deasupra axei sau sub axa, dar contează care grafic este MAI MARE(față de alt grafic), și care este JOS.

În exemplul luat în considerare, este evident că pe segment parabola este situată deasupra liniei drepte și, prin urmare, de la 2 x – x 2 trebuie scazut - x.

Soluția finalizată ar putea arăta astfel:

Cifra dorită este limitată de o parabolă y = 2x – x 2 deasupra și drepte y = -x de mai jos.

Pe segmentul 2 x – x 2 ≥ -x. Conform formulei corespunzătoare:

Răspuns: .

De fapt, formula școlară pentru aria unui trapez curbiliniu în semiplanul inferior (a se vedea exemplul nr. 3) este un caz special al formulei

.

Pentru că axa BOU dat de ecuaţie y= 0 și graficul funcției g(x) situat sub axă BOU, Asta

.

Și acum câteva exemple pentru propria dvs. soluție

Exemplul 5

Exemplul 6

Găsiți aria unei figuri delimitate de linii

Când rezolvați probleme care implică calcularea ariei folosind o integrală definită, se întâmplă uneori un incident amuzant. Desenul a fost făcut corect, calculele au fost corecte, dar din nepăsare... A fost găsită zona figurii greșite.

Exemplul 7

Mai întâi să facem un desen:

Figura a cărei zonă trebuie să o găsim este umbrită în albastru(uitați-vă cu atenție la starea - cum este limitată cifra!). Dar, în practică, din cauza neatenției, oamenii decid adesea că trebuie să găsească zona figurii care este umbrită în verde!

Acest exemplu este util și prin faptul că calculează aria unei figuri folosind două integrale definite. Serios:

1) Pe segmentul [-1; 1] deasupra axei BOU graficul este situat drept y = x+1;

2) Pe un segment deasupra axei BOU este situat graficul unei hiperbole y = (2/x).

Este destul de evident că zonele pot (și ar trebui) să fie adăugate, prin urmare:

Răspuns:

Exemplul 8

Calculați aria unei figuri delimitate de linii

Să prezentăm ecuațiile sub formă de „școală”.

și faceți un desen punct cu punct:

Din desen este clar că limita noastră superioară este „bună”: b = 1.

Dar care este limita inferioară?! Este clar că acesta nu este un număr întreg, dar ce este?

Pot fi, o=(-1/3)? Dar unde este garanția că desenul este realizat cu acuratețe perfectă, s-ar putea dovedi că o=(-1/4). Ce se întâmplă dacă am construit incorect graficul?

În astfel de cazuri, trebuie să petreceți timp suplimentar și să clarificați limitele integrării analitic.

Să găsim punctele de intersecție ale graficelor

Pentru a face acest lucru, rezolvăm ecuația:

.

Prin urmare, o=(-1/3).

Soluția ulterioară este banală. Principalul lucru este să nu vă confundați în înlocuiri și semne. Calculele de aici nu sunt cele mai simple. Pe segment

, ,

conform formulei potrivite:

Răspuns:

Pentru a încheia lecția, să ne uităm la două sarcini mai dificile.

Exemplul 9

Calculați aria unei figuri delimitate de linii

Soluție: Să reprezentăm această figură în desen.

Pentru a desena un desen punct cu punct trebuie să știți aspect sinusoide. În general, este util să cunoașteți graficele tuturor funcțiilor elementare, precum și unele valori sinusoidale. Ele pot fi găsite în tabelul de valori funcții trigonometrice. În unele cazuri (de exemplu, în acest caz), este posibil să se construiască un desen schematic, pe care graficele și limitele integrării ar trebui să fie în mod fundamental afișate corect.

Nu există probleme cu limitele de integrare aici, acestea decurg direct din condiția:

– „x” se schimbă de la zero la „pi”. Să luăm o altă decizie:

Pe un segment, graficul unei funcții y= păcatul 3 x situat deasupra axei BOU, De aceea:

(1) Puteți vedea cum sinusurile și cosinusurile sunt integrate în puteri impare în lecție Integrale ale funcțiilor trigonometrice. Ciupim un sinus.

(2) Folosim identitatea trigonometrică principală în formă

(3) Să schimbăm variabila t=cos x, atunci: este situat deasupra axei, prin urmare:

.

.

Nota: observați cum este luată integrala cubului tangentei aici un corolar al identității trigonometrice de bază

.